Radiation by an accelerated charge
Alternating magnetic field, electromagnetic radiation, electromagnetic induction
An electric field moves with the velocity that the particle had while emitting that field.
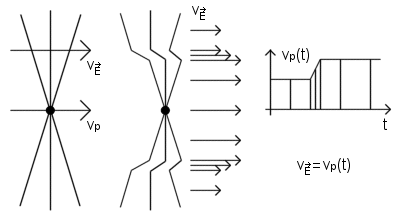
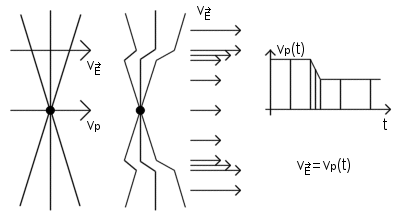
Electric field of a charge that stops
Suppose a charge q has been moving at constant speed v0 in the x direction for a long time. Suddenly it stops after a short period of constant deceleration. Electric field of a charge travels radially outward and moves with the velocity that the charge had while emitting that field.
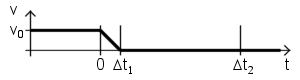
The velocity versus time graph
The electric field
Assuming that the v0 ≪ c, we can neglect the relativistic compression of the field lines. Time t=0 it was the moment when deceleration began, and position x=0 it was the position of the particle at that moment. The particle has been moved a little farther on before coming to a stop, Δx=1/2*v0Δt1. That distance is very small compared with the other distances in the picture.
We now examine the electric field at a time t=Δt2≫Δt1. The electric field reaches a distance R=cΔt2. Thus, the field at a distance greater than R=cΔt2, in region I must be a field of a charge which has been moving and is still moving at the constant speed v0. That field appears to come from the point x=v0Δt2 on the x axis. That is where the particle would be now if it hadn't stopped. On the other hand, the field at a distance less than c(Δt2-Δt1), in region II must be a field of a charge at rest close to the position x=0 (exactly at x=1/2*v0Δt1).
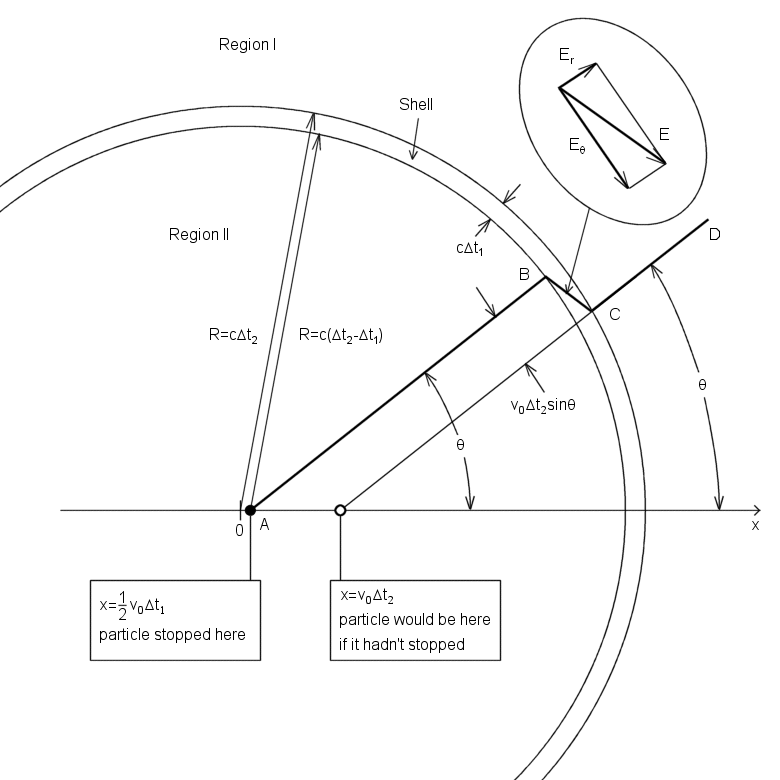
What must the field be like in the transition region, the spherical shell of thickness cΔt1 between region I and region II? A field line segment AB lies on a cone around the x axis which includes a certain amount of flux from the charge q. Due to the Gauss' law, if CD makes the same angle θ with the axis, the cone on which it lies includes that same amount of flux. (Because the v0 ≪ c, we can neglect the relativistic compression of the field lines.) That's why AB and CD must be parts of the same field line, connected by a segment BC. The line segment BC shows us the direction of the filed E within the shell. This field E within the shell has both a radial component Er and a transverse component Eθ. From the geometry of the figure their ratio is easily found.
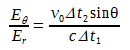 (1)
(1)Due to the Gauss' law, Er must have the same value within the shell thickness that it does in region II near B. That's why Er=q/4πε0R2=q/4πε0c2Δt22, and substituting this in Eq. 1 we obtain
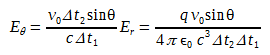 (2)
(2)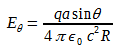 (3)
(3)We now calculate the energy stored in the transverse electric field above, in the whole spherical shell. The energy density is
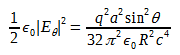 (4)
(4)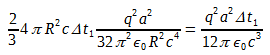 (5)
(5)Total energy in transverse electromagnetic field is
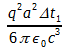 (6)
(6)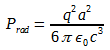 (7)
(7)radiation, accelerated, charge, electromagnetic, induction, wave, waves, physics, science,
Radiating Charge simulation - PhET INTERACTIVE SIMULATIONS
Purcell appendix B in the CGS system
